Binary Code Explained: What It Is And Why Computers Depend On It

If you don't already know how computers work, it may seem like an unapproachable subject. It's the kind of high-level science and math that can seem inaccessible to the average person. Though things can indeed get pretty complicated, the core of computing is mostly just simple things happening on a massive scale. So, if you ready your brain to accept that scale, there's a lot you can learn and understand without needing a fancy education or innate mathematical talent.

Binary code is the perfect place to start — it's conceptually simple but practically complex, and to computers, it's everything. Binary is the power behind the 4K YouTube video you're watching, the smartphone in your pocket, the servers keeping the internet on, and banking software ensuring your money is secure. So, let's look at exactly what binary is, what they do with it, and why it's so important.

The first thing to know about binary is that it's a counting system. Just like we use the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 to express all the numbers in existence, the binary counting system uses zeros and ones to express these same numbers. Our usual system is called decimal, or base 10, and counts in chunks of 10. The binary system, also known as base two, counts in chunks of two. As an example, let's count this collection of asterisks:

✱ ✱ ✱ ✱ ✱

Using the base 10 counting system, we'd express this number as five (5). Using the base two counting system, we'd express it as 101. While they look very different, both versions refer to the same amount of asterisks.

So, if they're doing the exact same job, then what is the point of having two different systems? Well, counting systems are extremely contextual — the way they work is based on what's convenient and natural for the entity that's doing the counting. Humans chose base 10 because we have 10 fingers and use those fingers to help us count. We have unique symbols for 0 to 9, and when we pass 9, we add a 1 to the front and cycle back through.

If we had six fingers, we'd have unique symbols for 0 to 5, and then add a 1 to the front and cycle back through. In other words, in base six, "10" would equate to our number six.

So, if humans chose base 10 to count in because they have 10 fingers, who would choose to count in base two? Perhaps a turtle because they only have two fingerless flippers. Or a penguin because they only have two fingerless wings. Or a computer, because the teeny tiny components that make up a computer only have two states — on (1) or off (0).

At their core, computers are machines that use electrical current to flip switches. Each switch can only ever be on or off; there are no other outcomes. This means that if a computer wants to count, it's restricted to base two. It has two digits — 0 and 1 — and when it passes 1, it has to add 1 to the front and cycle back through. In other words, as strange as it may seem, one is 1, and two is 10. Using binary, this is what we get with the first five numbers:

• Zero = 0
• One = 1
• Two = 10
• Three = 11
• Four = 100
• Five = 101

In this system, digits are switches, and you can store any number you want as long as you have enough switches to express it. If you had eight switches, for example, you could write any number in binary between 0 and 255. 0 would look like 00000000, and 255 would look like 11111111. If you wanted to go to 256, you'd need to add an extra switch to represent the extra digit — 100000000.

We now know that we can configure a bunch of switches to represent a number in binary — but what exactly is the use of that? How do we use, manipulate, or add it to another number? The answer is something called logic gates.

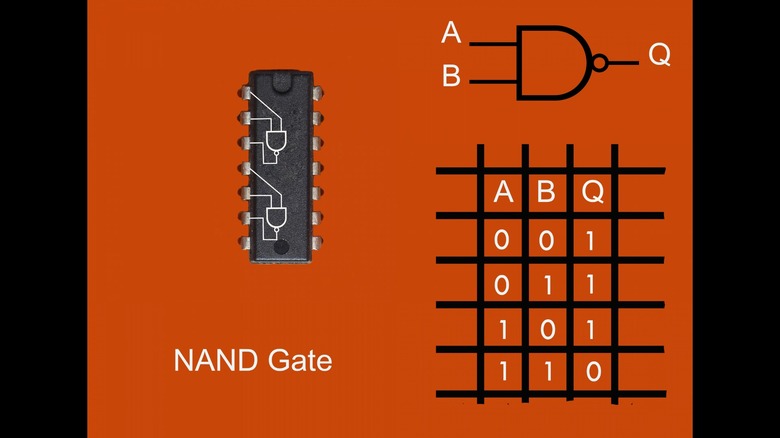
As the name suggests, logic gates can open and let an electrical current pass through or close and block its path. There are different types of gates, such as AND, OR, XOR, or NAND, and they all have different requirements that you need to meet to open them. The open-or-closed result that a gate produces is called its output — and if you assign numbers to these outputs, 0 is closed (blocked current), and 1 is open (flowing current).

While gates usually only have one output, many have multiple inputs — two or more electrical currents coming from different places. The combination of inputs it receives (0s for no current and 1s for flowing current) plus the purpose of the gate (OR, AND, etc) is what determines the output.

Let's take an AND gate as an example — it has two inputs and one output. For the gate to output 1, the inputs need to be 1 AND 1. Anything else, and the output will be 0. For an OR gate to open, one input OR the other needs to be 1. If neither is 1, or both are 1, it stays closed.

While what logic gates can do is pretty cool, in isolation, it can be difficult to imagine a practical application. However, if you combine gates of the right type, in the right numbers, and in the right order, you can add two numbers together. Admittedly, it takes hundreds of gates to pull this off, so it's a tad complex and a little too much to explain here. But it can be done! The device you're reading this article on is the proof — because once you have the power to express numbers and add them together, you have the power to do (pretty much) anything!

This sounds dramatic, but it's kind of true. Computers can add numbers together but can't subtract, divide, or multiply — not directly, anyway. They use addition to emulate other mathematical operations in long-winded, roundabout ways. But since they can pull off millions of tiny computations every second, what sounds long-winded in explanation takes no time at all to actually happen.

Still, carrying out sums with binary numbers feels like a long, long way from making video games or plotting a course to the moon. How do any number of simple mathematical operations end up producing such complex results? Well, it just does. It's hard to wrap your head around since your head simply can't fit that many tiny operations in it all at once — let alone keep track of the larger picture they're painting — but it's true.

We started by looking at binary as a counting system, which it is — but that's not the only thing it can do. Since it's the only thing we can use to communicate with computers, we use it to encode all sorts of different information. One obvious example is text. A computer can't read the word "hello" like we can, so each character has to have a binary code that represents it.

The first character encoding standard for computers was called ASCII, and if we write "hello" in ASCII, it looks like this: 01101000 01100101 01101100 01101100 01101111. When humans want to read ASCII, however, it's commonly represented in a different code with better readability, so "hello" can also look like this: 68 65 6C 6C 6F.

Character encoding systems are limited by the number of bits they use — i.e., the number of binary digits. The first versions of ASCII used 7-bit codes, which meant they could attach a character to every binary number between 0000000 and 1111111, which is 0 to 128 in decimal. With 128 slots to fill, they were able to include lowercase characters, uppercase characters, numbers, and plenty of symbols and punctuation.

This kind of coding system isn't new, by the way — braille and Morse code are binary, too. Braille dots are either raised or flat, and Morse code is dots or dashes.

Earlier, it was mentioned that humans can't keep track of the billions of operations happening inside a computer — but if so, how do programmers do it? The answer is, of course, they don't. They don't need to know which gates are producing which outputs or what number 1010000110101010 is in decimal because all of that is happening many layers below the programmer's domain.

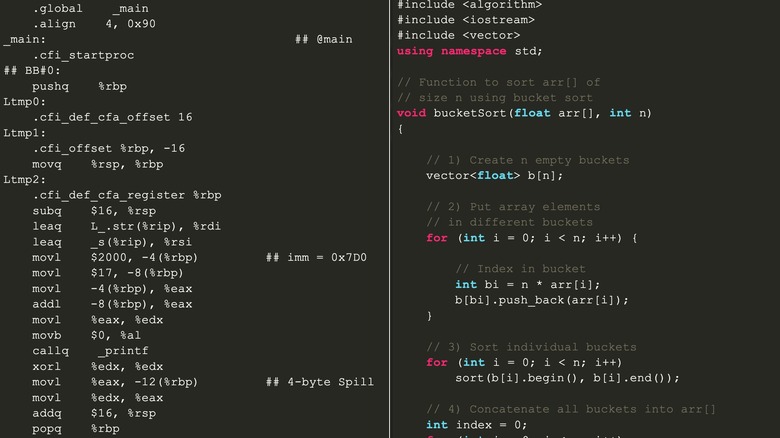
As you probably already know, programmers and software engineers write in programming languages like C++, C#, Python, and JavaScript. These languages are designed to be understandable, readable, and writable for humans — and only after the humans are done with them are they translated into a binary data format that the computer can read and execute.

Programming languages like this are called "high-level" languages, and the closer you get to the inner workings of the hardware itself, the more "low-level" things become. Some engineers do use low-level languages like assembly code — but even this doesn't require typing out 0s and 1s. If you look at the picture above, you can see some C++ code on the right and assembly code on the left.

Even though we don't see it as computer users and many programmers don't see it much either, binary code is the lifeblood of computers. On or off, open or closed, current or no current, 1 or 0 — however you look at it, these two states are the only things computers can read and the only things they can output. But thanks to the magic of math and the versatility of information encoding, the applications are mind-bogglingly diverse.

This is just a surface-level discussion of binary and how computers work since the topic is, unsurprisingly, huge and complex. It's not that difficult — everyone has what it takes to understand it — there's just a lot to cover. If you're curious about binary and logic gates and how they become a computer, there's a book for that. In the meantime, now that you know a little about binary numbers and how they work, here's a joke to celebrate: There are 10 types of people in the world — those who understand binary and those who don't.